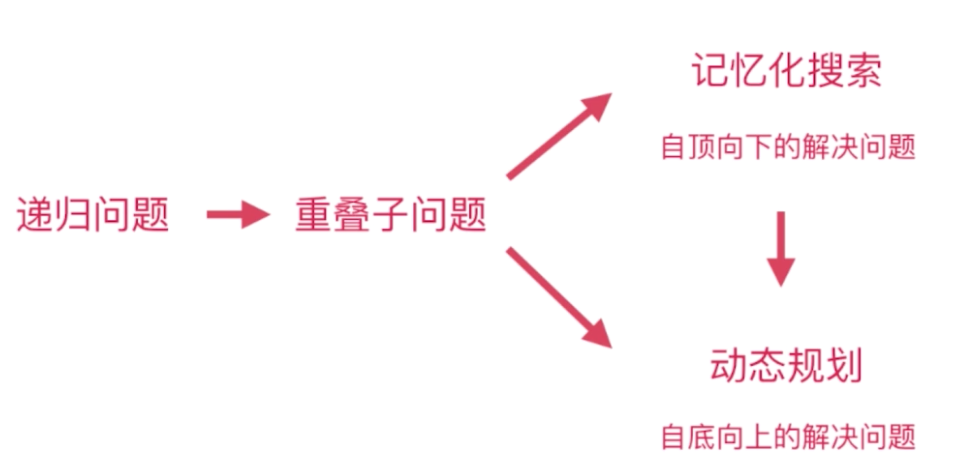
9-1 什么是动态规划

将原问题拆解成若干个子问题，同时保存子问题的答案，使得每个子问题只求解一次，最终获得原问题的答案

举例斐波那契额数列

F(0) = 1, F(1) = 1, F(n) = F(n-1) + F(n-2)

int fib(int n){
    if(n ==0) return 0;
    if(n ==1) return 1;
    return fib(n-1) + fib(n-2);
}

这个程序的时间复杂度是指数级的， 2的n次方

以 n = 5 为例，当n=5时，fib(5)的计算过程如下:

1. fib(5)
2. fib(4) + fib(3)
3. (fib(3) + fib(2)) + (fib(2) + fib(1))
4. ((fib(2) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))
5. (((fib(1) + fib(0)) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))

在求f(5)的时候，f(3) 被重复计算了两次

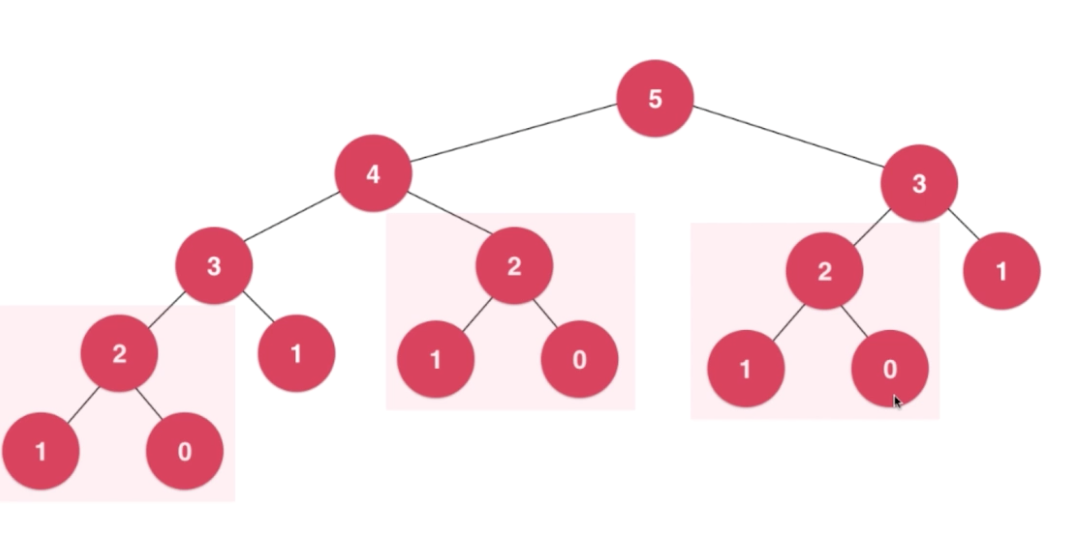
在求f(5)的时候，f(2) 被重复计算了三次

想象一下，

如果是计算f(100)的话，就会出现非常多重复计算的情况。

所以就有一个非常自然的想法： 对于这些重复的计算，我们有没有可能只计算一次？

/* 
 * 基础解法,按照递归方法求解,该算法的运算时间是指数级增长的 
 * 这种算法对于相似的子问题进行了重复的计算，因此不是一种高效的算法 
 */  
public class FibonacciRecursion {  

    //-----------计算Fibonacci数列值的递归函数--------------  
    public static int fib(int n){  
        if(n==1||n==2){//序列中第1,2个数为1  
            return 1;  
        }  
        return fib(n-1)+fib(n-2);  
    }  

    public static void main(String[] args) {  
        int i=46;  
        long begin=System.currentTimeMillis();  
        System.out.println("fib("+i+"):"+fib(i));  
        long cost=System.currentTimeMillis()-begin;  
        System.out.println("耗时:"+cost+"ms");  
    }  
}

/* 
 * 可以通过保存已经算出的子问题的解来避免重复计算 
 * 即使用动态规划的技术 
 */  
public class FibonacciDP {  

    // ----------使用动态规划(DP)求fibonacci数列的值------------  
    public static int fib(int n) {  
        int[] array = new int[n];//用来保存动态规划过程中的状态  
        array[0] = 0;  
        array[1] = 1;  
        for (int i = 2; i < n; i++)  
            array[i] = array[i - 1] + array[i - 2];//动态规划的状态转移式  
        return array[n-1];  
    }  

    public static void main(String[] args) {  
        long begin=System.currentTimeMillis();  
        System.out.println("fib(46):"+fib(46));  
        long cost=System.currentTimeMillis()-begin;  
        System.out.println("耗时:"+cost+"ms");  
    }  
}