Subsets

Given a set of distinct integers, nums, return all possible subsets (the power set).

Note:The solution set must not contain duplicate subsets.

For example,
If nums=[1,2,3], a solution is:

[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

分析

回溯法可用图示和函数运行的堆栈图来理解，强烈建议使用图形和递归的思想分析，以数组[1, 2, 3]进行分析。下图所示为list及result动态变化的过程，箭头向下表示list.add及result.add操作，箭头向上表示list.remove操作。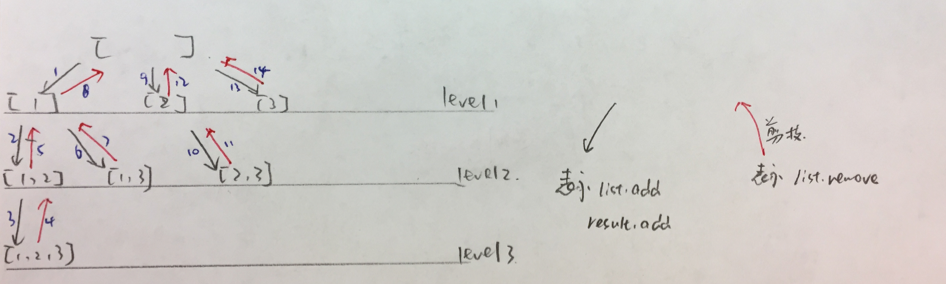

// 递归：实现方式，一种实现DFS算法的一种方式
class Solution {
    /**
     * @param S: A set of numbers.
     * @return: A list of lists. All valid subsets.
     */
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> results = new ArrayList<>();

        if (nums == null) {
            return results;
        }

        Arrays.sort(nums);
        helper(new ArrayList<Integer>(), nums, 0, results);
        return results;
    }


    // 递归三要素
    // 1. 递归的定义：在 Nums 中找到所有以 subset 开头的的集合，并放到 results
    private void helper(ArrayList<Integer> subset,
                        int[] nums,
                        int startIndex,
                        List<List<Integer>> results) {
        // 2. 递归的拆解
        // deep copy
        // results.add(subset);
        results.add(new ArrayList<Integer>(subset));

        for (int i = startIndex; i < nums.length; i++) {
            // [1] -> [1,2]
            subset.add(nums[i]);
            // 寻找所有以 [1,2] 开头的集合，并扔到 results
            helper(subset, nums, i + 1, results);
            // [1,2] -> [1]  回溯
            subset.remove(subset.size() - 1);
        }

        // 3. 递归的出口
        // return;
    }
}

代码

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        //special case 
        if (nums == null) {return result;}
        dfs(nums, 0, new ArrayList<Integer> (), result); 
        return result;
    }

    public void dfs(int[]nums, int index, List<Integer> path, List<List<Integer>> result) {
        result.add(new ArrayList<Integer>(path));
        for (int i = index; i < nums.length; i++) {
            path.add(nums[i]);
            dfs(nums, i + 1, path, result);
            //剪枝
            path.remove(path.size() - 1);
        }
    }
}